 |
CWO++library
0.32
|
 |
CWO++library
0.32
|
Functions | |
| void | CWO::Re () |
| Taking only the real part of complex amplitude. | |
| void | CWO::Im () |
| Taking only the imaginary part of complex amplitude. | |
| void | CWO::Conj () |
| Calculating the complex conjugation of complex amplitude. | |
| void | CWO::Intensity () |
| Calculating the absolute square (light intensity) of complex amplitude. | |
| void | CWO::Amp () |
| Calculating the amplitude of complex amplitude. | |
| void | CWO::Phase (float offset=0.0f) |
| Calculating complex amplitude with the constant amplitude . | |
| void | CWO::Arg (float scale=1.0f, float offset=0.0f) |
Calculating the argument of complex amplitude with real value from 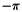 to to 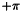 . .. | |
| void | CWO::Expi () |
| void | CWO::Arg2Cplx (float scale=1.0, float offset=0.0) |
| void | CWO::Cart2Polar () |
| void | CWO::Polar2Cart () |
| void | CWO::ReIm (CWO &re, CWO &im) |
| replace the real and imaginary parts. | |
| void CWO::Re | ( | ) |
| void CWO::Im | ( | ) |
Taking only the imaginary part of complex amplitude.
@note
![$ Re[a] \leftarrow Im[a] $](form_4.png)
![$ Im[a] \leftarrow 0 $](form_3.png)
| void CWO::Conj | ( | ) |
Calculating the complex conjugation of complex amplitude.
@note
![$ Re[a] \leftarrow Re[a] $](form_2.png)
![$ Im[a] \leftarrow -Im[a]$](form_5.png)
| void CWO::Intensity | ( | ) |
Calculating the absolute square (light intensity) of complex amplitude.
@note
![$ Re[a] \leftarrow Re[a]^2+Im[a]^2 $](form_6.png)
![$ Im[a] \leftarrow 0 $](form_3.png)
| void CWO::Amp | ( | ) |
Calculating the amplitude of complex amplitude.
@note
![$ Re[a] \leftarrow \sqrt{Re[a]^2+Im[a]^2} $](form_7.png)
![$ Im[a] \leftarrow 0 $](form_3.png)
| void CWO::Phase | ( | float | offset = 0.0f | ) |
Calculating complex amplitude with the constant amplitude .
@param offset : adjust the phase distribution @note
![$ \theta=\tan^{-1}\frac{Im[a]}{Re[a]} $](form_8.png)
![$ Re[a] \leftarrow \cos(\theta) $](form_9.png)
![$ Im[a] \leftarrow \sin(\theta) $](form_10.png)
| void CWO::Arg | ( | float | scale = 1.0f, |
| float | offset = 0.0f |
||
| ) |
Calculating the argument of complex amplitude with real value from 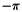 to
to 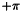 .
.
.
@param scale : adjust scale, ex. if setting scale=1.0, the phase range is \f-$\pi\f to + \form#21. if setting scale=1/\f-2$\pi\f, the phase range is -0.5 to +0.5. @param offset : adjust the phase range, ex. if setting offset=CWO_PI, the phase range in the phase distribution is 0 to \form#13. @note
![$ Re[a] \leftarrow tan^{-1}(\frac{Im[a]}{Re[a]})+offset $](form_14.png)
![$ Im[a] \leftarrow 0 $](form_3.png)
| void CWO::Expi | ( | ) |
I do not recommend to use this function. I will abolish the function in future CWO++ library.
| void CWO::Arg2Cplx | ( | float | scale = 1.0, |
| float | offset = 0.0 |
||
| ) |
Convering argument (real value) to complex amplitude.
Concreately, the following calculation is done.
@param offset : .
@note
![$ Re[a] \leftarrow tan^{-1}(\frac{Im[a]}{Re[a]})+offset $](form_14.png)
![$ Im[a] \leftarrow 0 $](form_3.png)
replace the real and imaginary parts.
@param re : @param im : @note CWO a @n
![$ Re[a] \leftarrow Re[re] $](form_15.png)
![$ Im[a] \leftarrow Re[im] $](form_16.png)
 1.8.1
1.8.1